Graph rewrites, from emergent algebras to chemlambda. © Marius Buliga (2020-2024), http://imar.ro/~mbuliga/chemlambda-github/history-of-chemlambda.html
Context
The chemlambda project context and relevant previous work are explained in Section 4 (About this project) of [arXiv:2003.14332]. See also, for more mathematical background,the presentation[Emergent rewrites in knot theory and logic. Marius Buliga (2020), https://mbuliga.github.io/novo/presentation.html]
Here I report about the modifications of the various formalisms which appeared under the name chemlambda.
Contents
Graphic lambda calculus
Chemlambda v1 (chemical concrete machine)
Chemlambda v2
Interaction Combinators, as they appear in chemlambda v2 programs
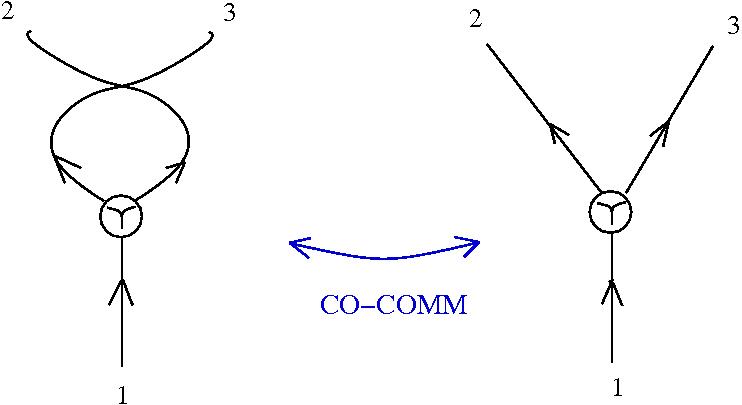
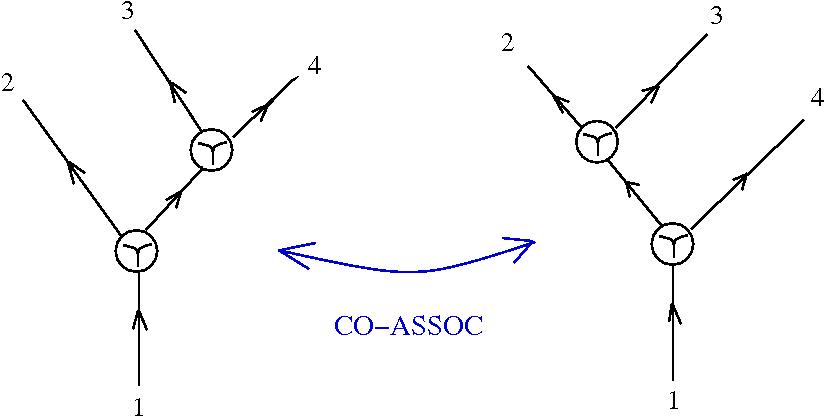
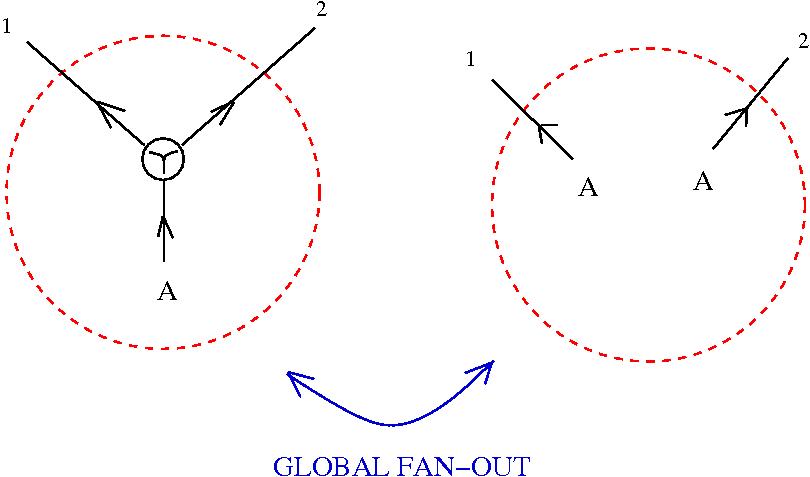
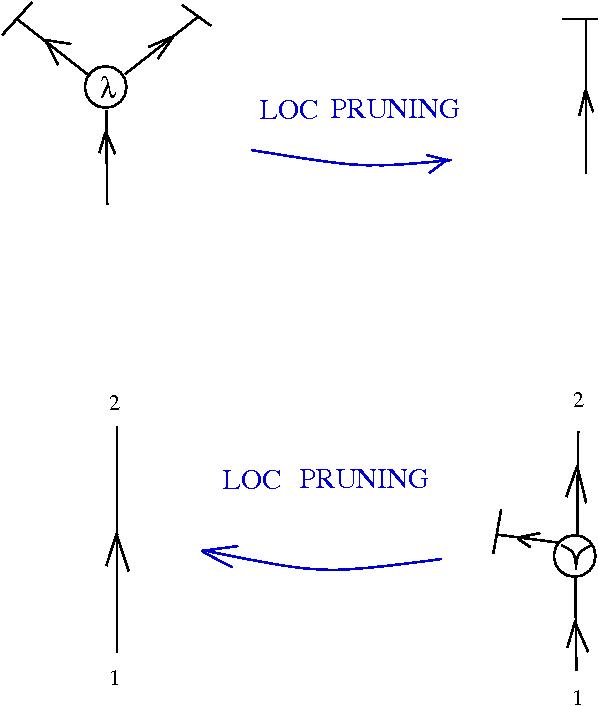
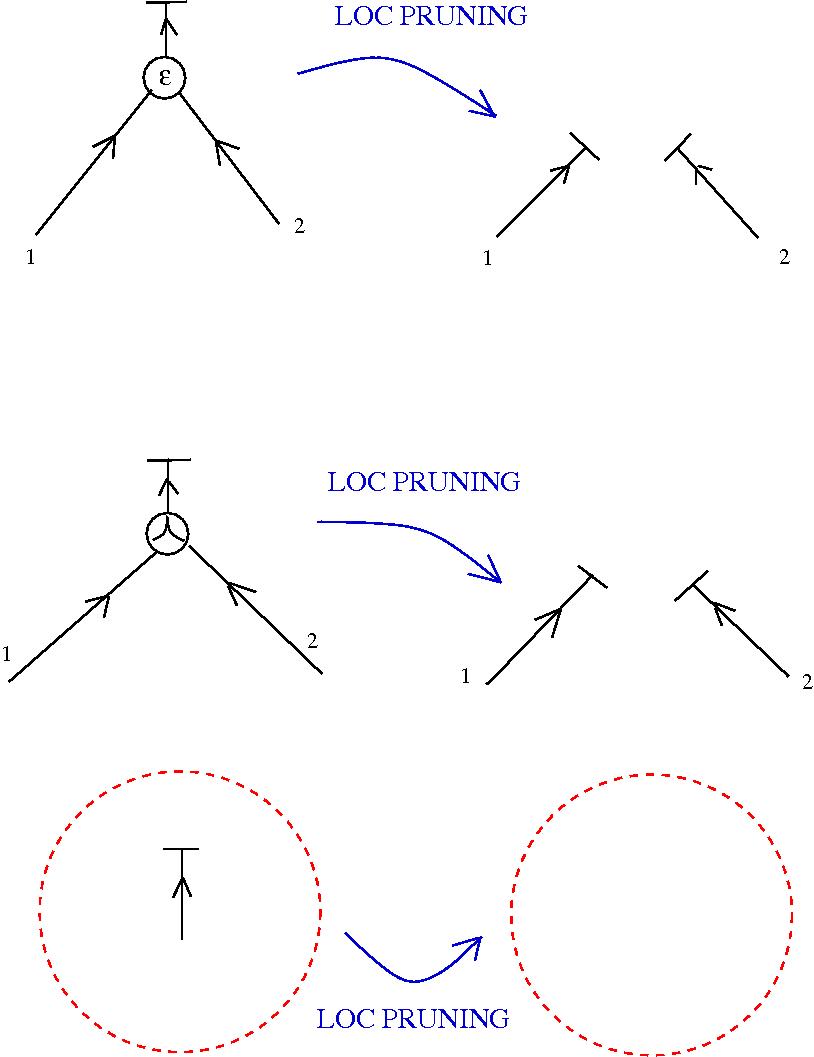
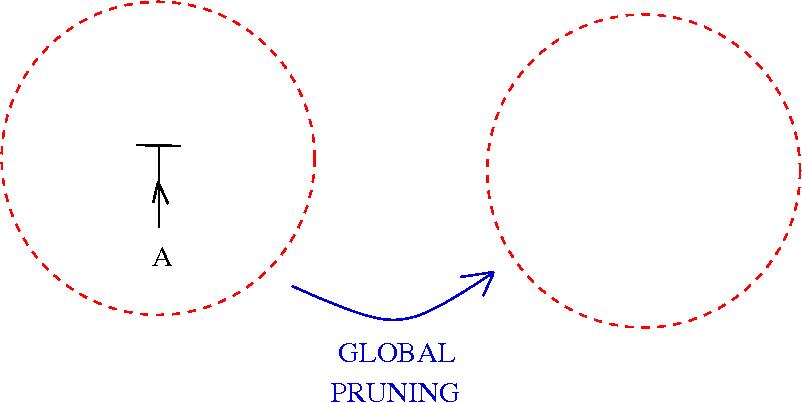
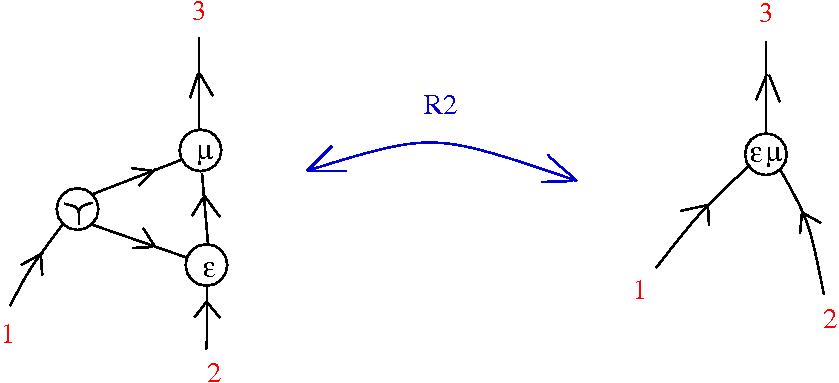
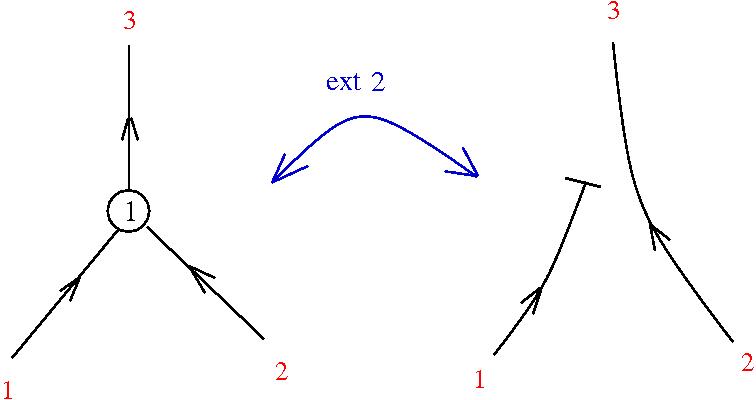
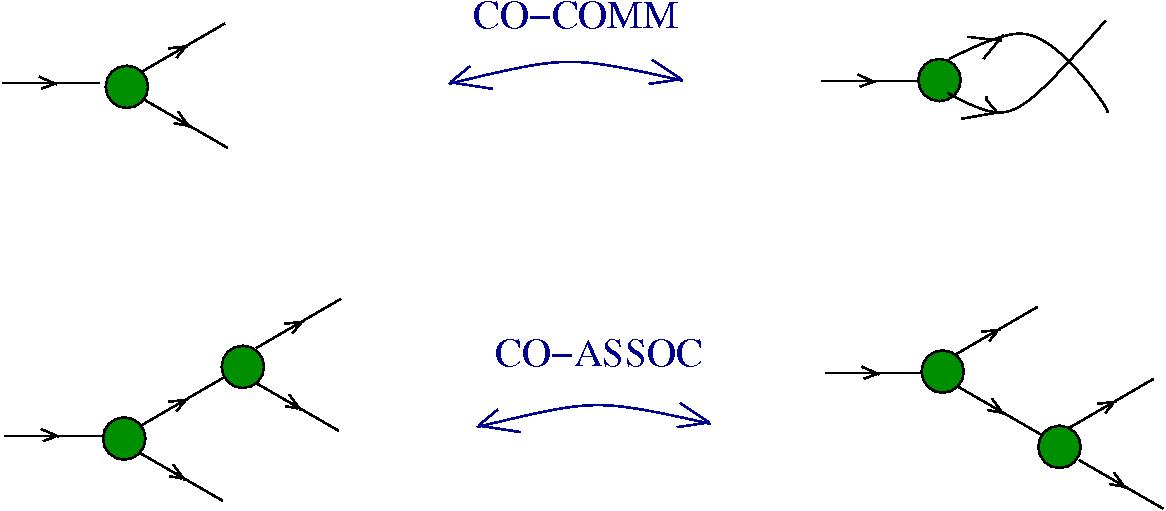
Graphic lambda calculus
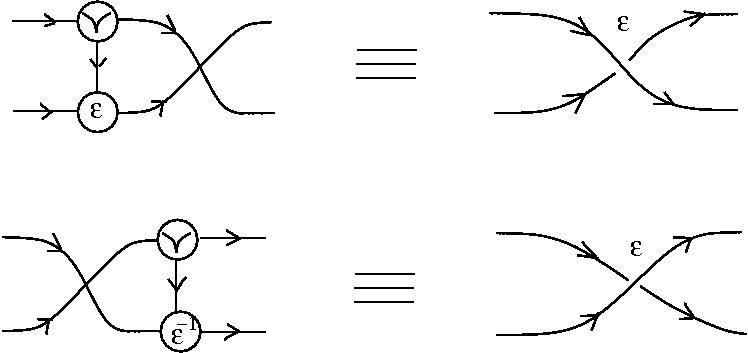
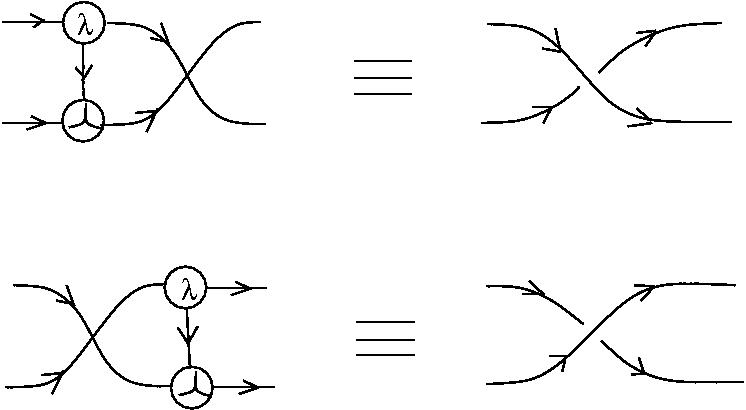
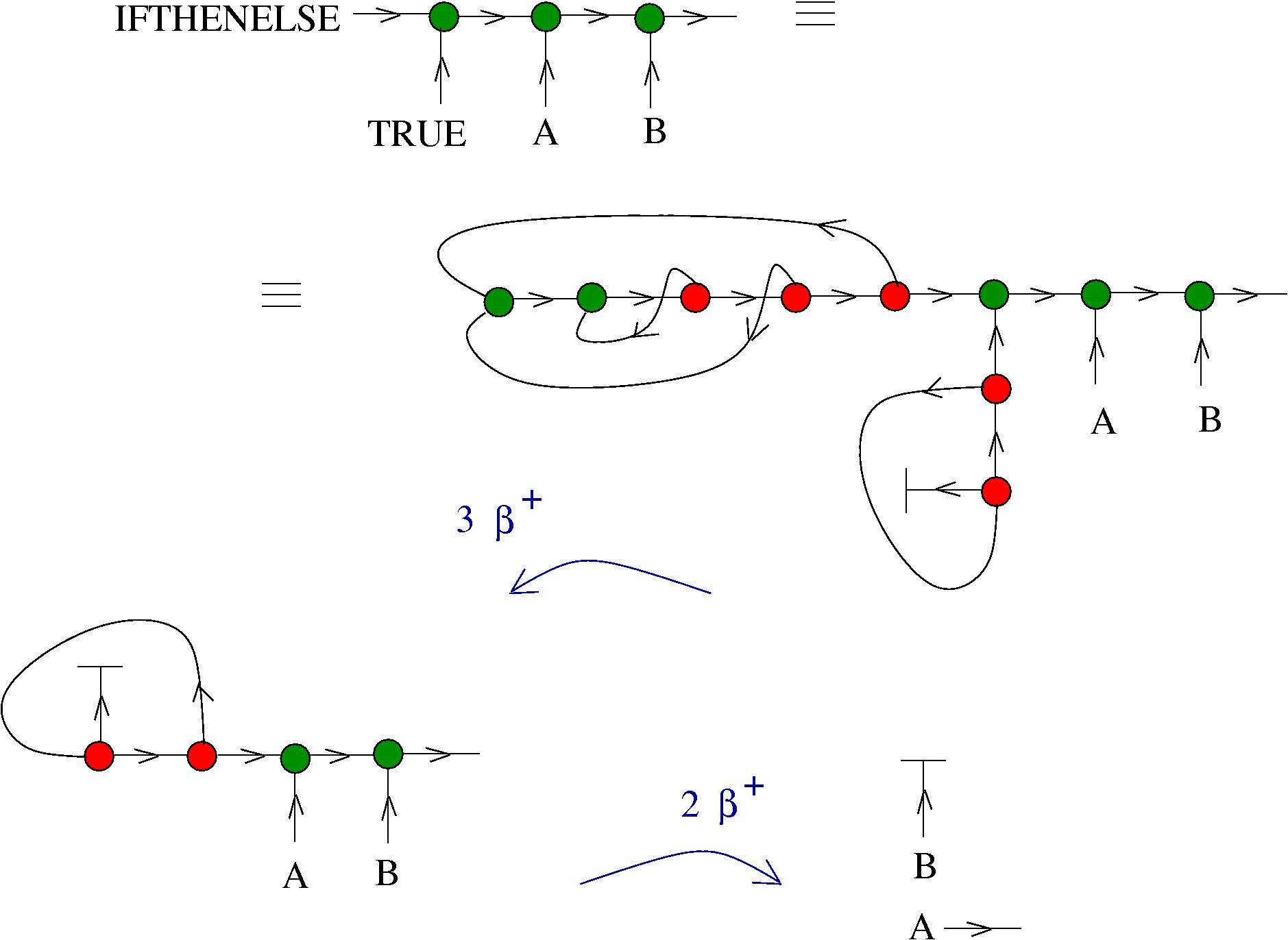
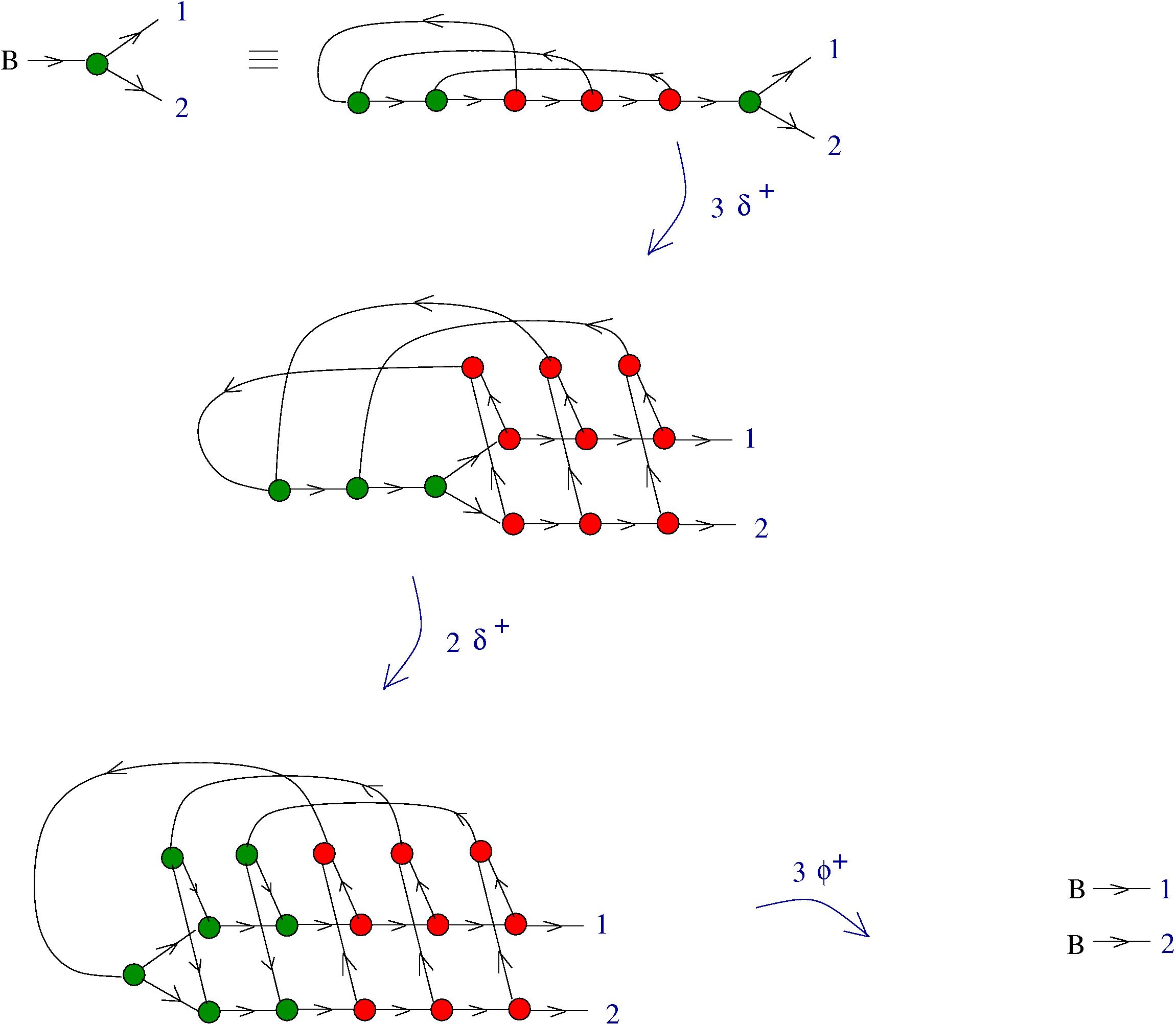
[arXiv:1305.5786]There is an algorithm for conversion of untyped lambda terms into glc graphs. Here are two examples of reductions:
- reduction of the Omega combinator
This is done via the identification of decorated crossings as
More precisely, here a tangle diagram is an oriented port graph in the sense of Bawden, with nodes which are 4-valent and oriented links. The nodes can be either undecorated, i.e. of the two kinds of oriented crossings, or decorated, i.e. the two kinds of decorated crossings are supplementary decorated with an element of a commutative group.
The difference from usual (oriented and with decorated crossings) tangle diagrams is that as graphs these diagrams are not supposed to be planar. By Kuratowski theorem, a graph is planar if it does not contain certain local patterns. In the terms of local machines explained in
[Alife properties of directed interaction combinators vs. chemlambda. Marius Buliga (2020), https://mbuliga.github.io/quinegraphs/ic-vs-chem.html#icvschem]
we can't detect with a local machine the absence of a local pattern in a graph, only the presence of it.
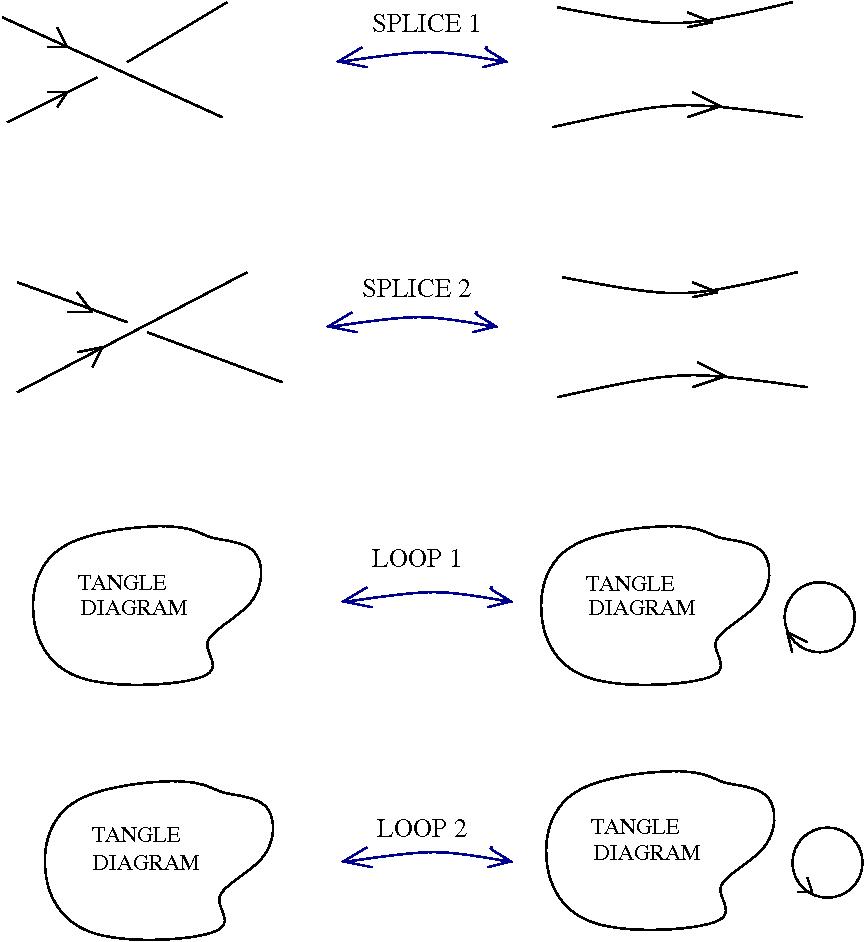
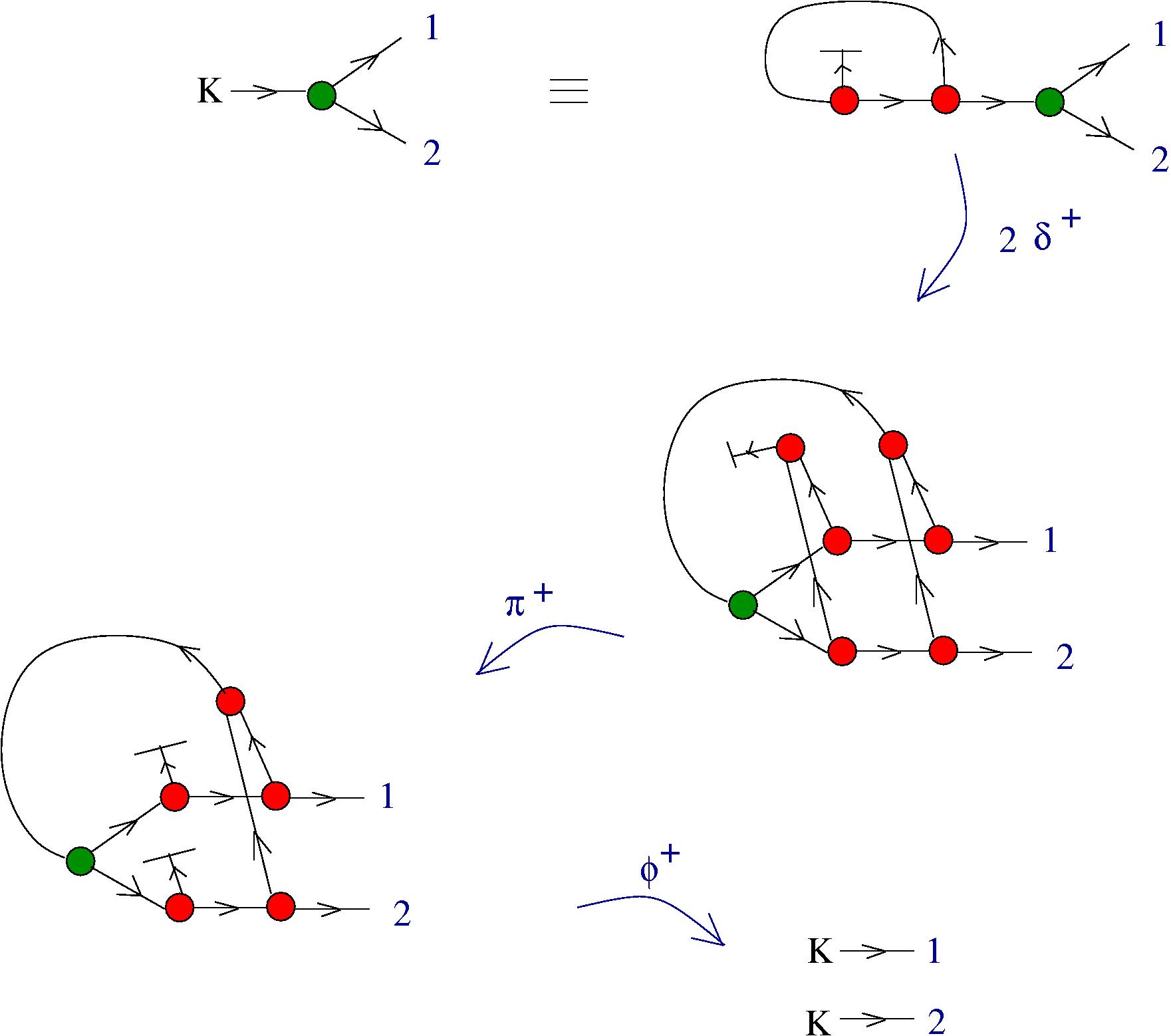
Under this identification the equivalent of the beta rewrite in terms of tangle diagrams becomes equivalent with the "splice" and "loop" graph rewrites
Chemlambda v1 (chemical concrete machine)
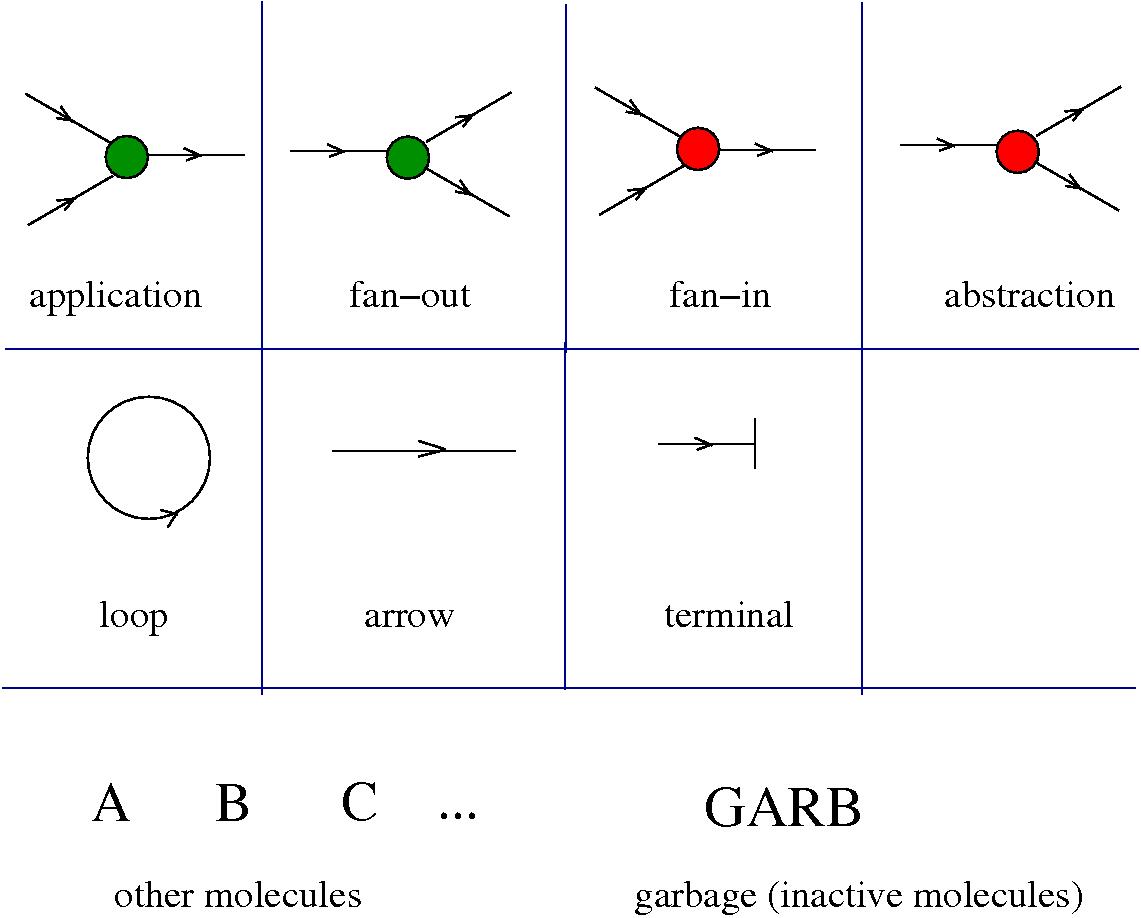
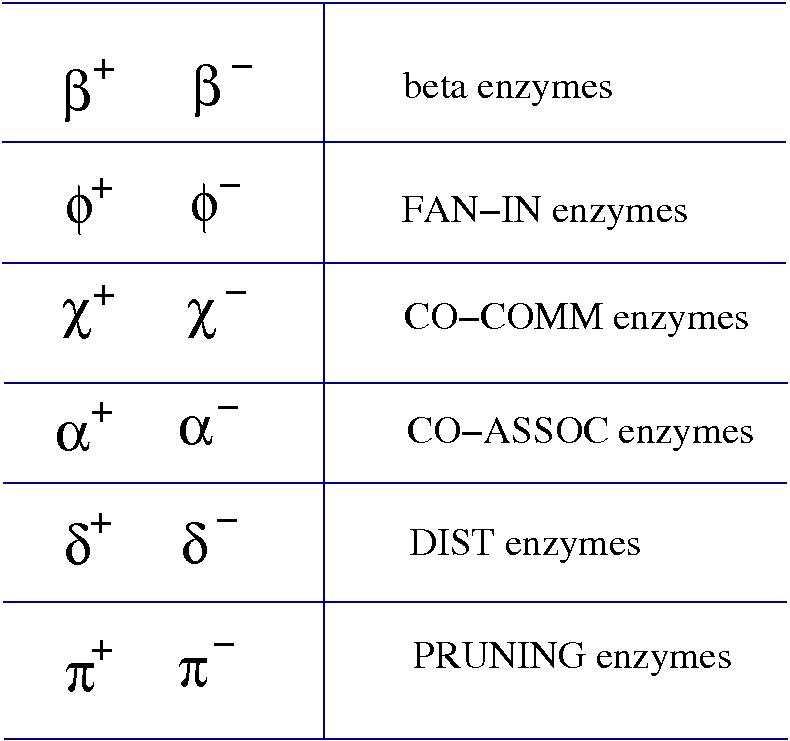
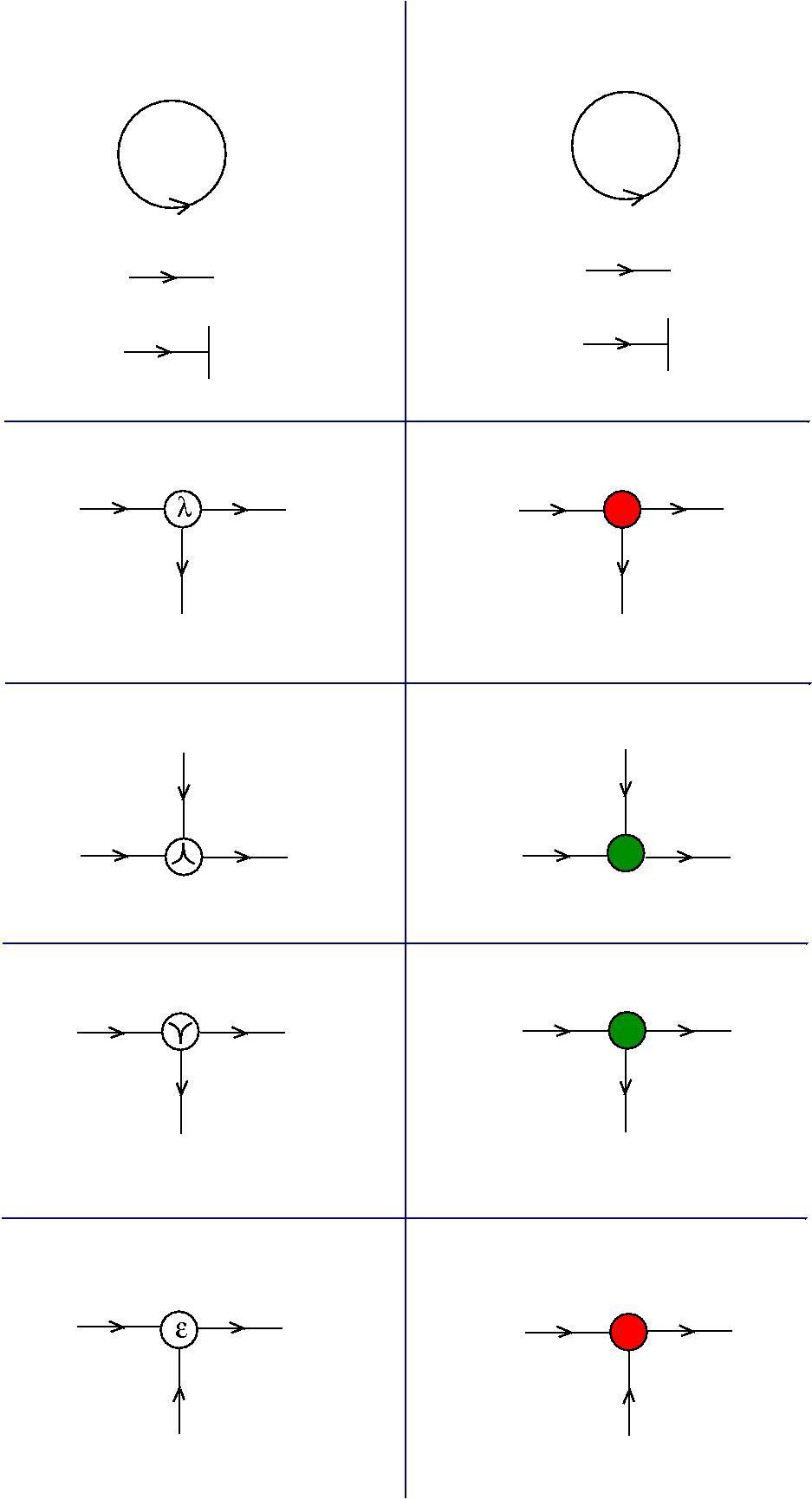
[arXiv:1309.6914]The elements of chemlambda v1 are
The first published (in the usual ways) article which contains the name "chemlambda" is joint with L.H. Kauffman, in the ALIFE-14 conference, [arXiv:1403.8046]. Here Kauffman pushes again for a more topological version [Kauffman' slides] which mixes tangle diagrams with chemlambda nodes, in order to be able to do computations (in the logical sense).The emergent algebras part of GLC, which is still present in chemlambda, used such tangle diagrams manipulations for differential calculus computations, instead. In these articles the emergent algebras aspects and interest are hidden.
Together with Kauffman, we experimented a lot with the power of chemlambda v1. Our essays on paper were not going too far, due to the lack of a program which could make much easier such exploration. In the background this was because of a lack of a clear rewrite application algorithm.
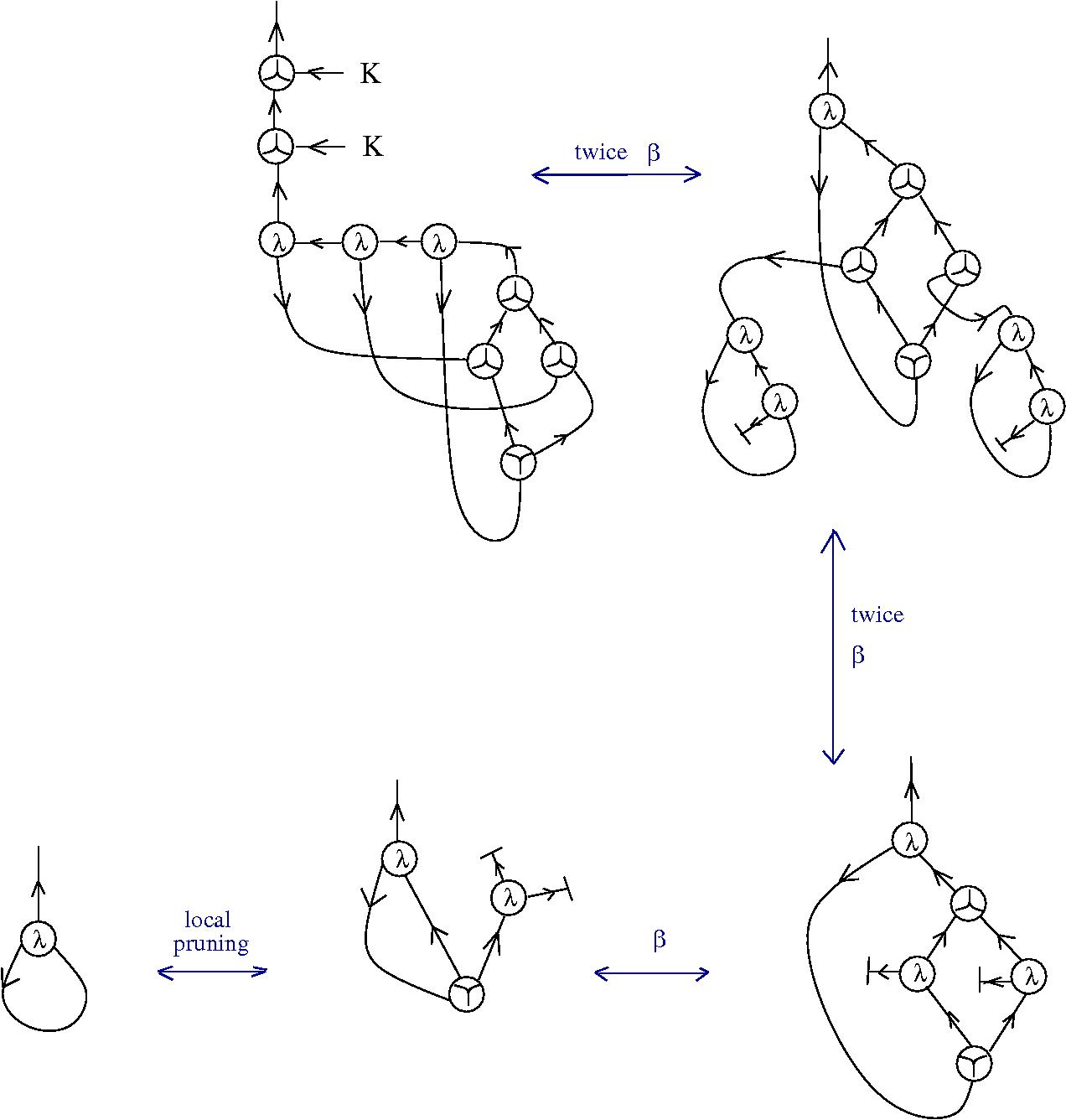
During this period I became aware of the existence of chemlambda quines. See as an example the tedious manipulation of reductions for the predecessor of a Church number taken from [this chorasimilarity post]
Chemlambda v2
is an artificial chemistry, in the sense that it is a purely local graph rewrite system together with an algorithm of applications which can be done by local machines. See [arXiv:2005.06060] for more explanations.Motivated by the first programming essays by Kauffman for chemlambda v1, I wrote the needed programs for chemlambda v2, in awk and html+d3.js used for visualization. The first chemlambda project site contains demonstrations made with these programs. The github repository is chemlambda-gui.
The latest chemlambda project site, which contains several repositories from various contributors, is this. With the help of contributors, now we can reduce chemlambda molecules directly in js, as you can see in the more recent demonstrations.
Chemlambda can now be compared with Interaction Combinators and there is a lambda calculus to chemlambda parser and reducer.
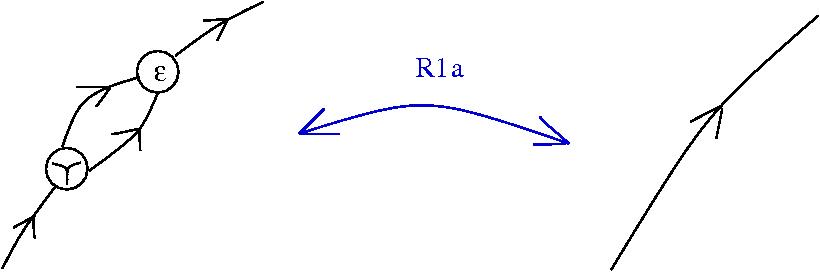
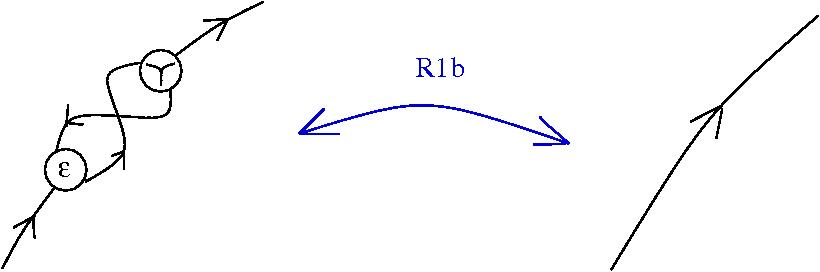
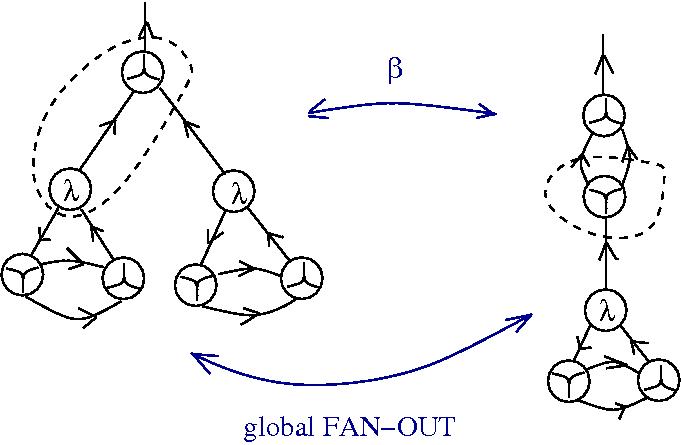
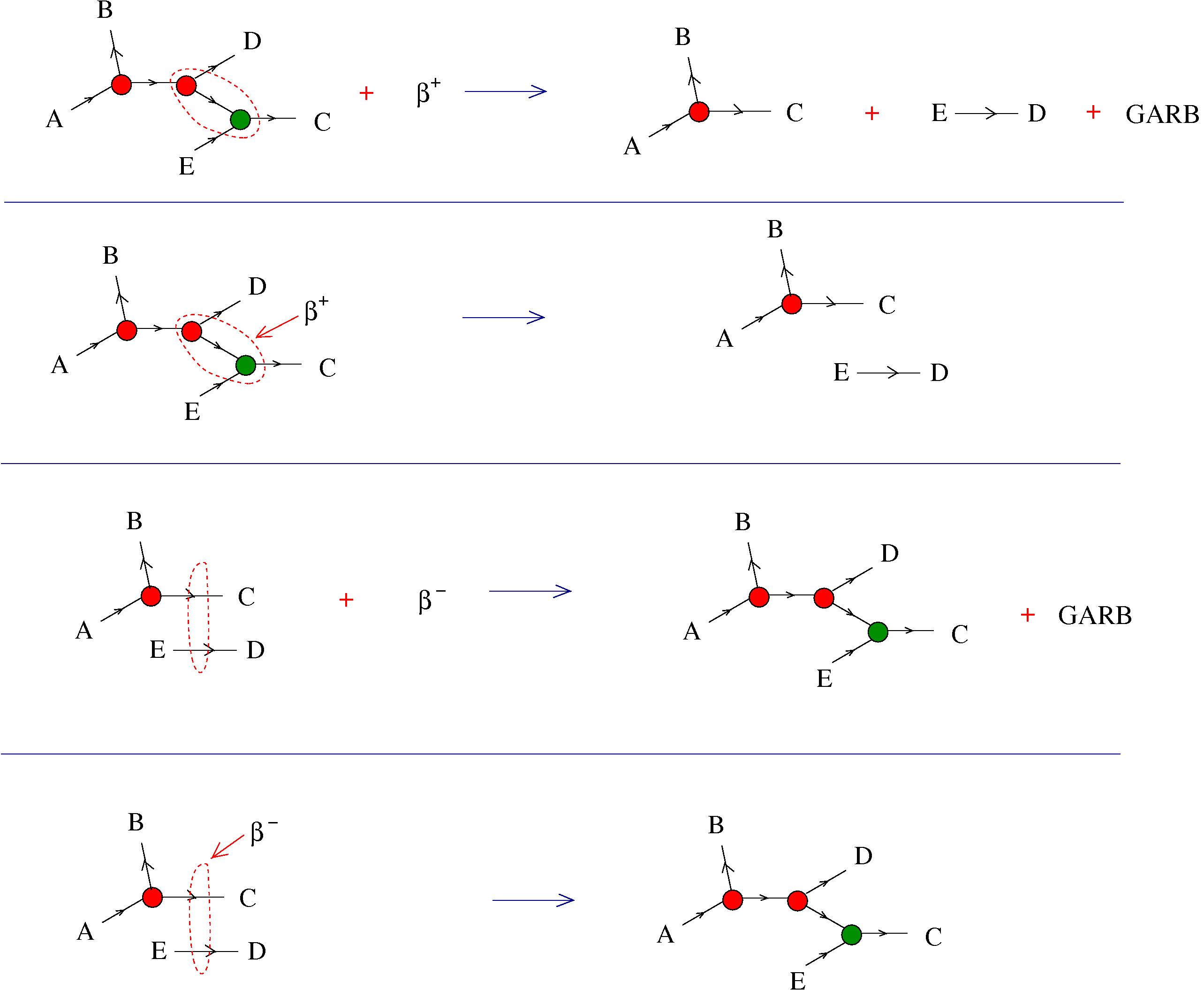
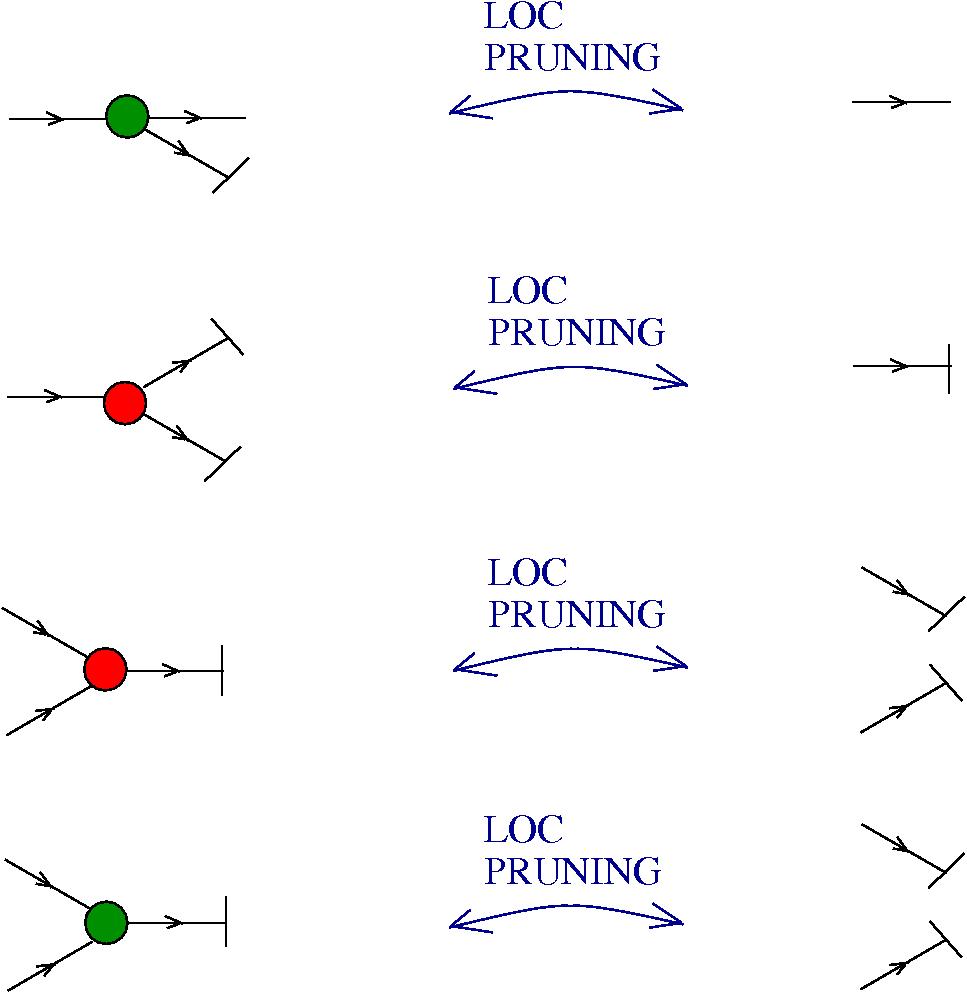
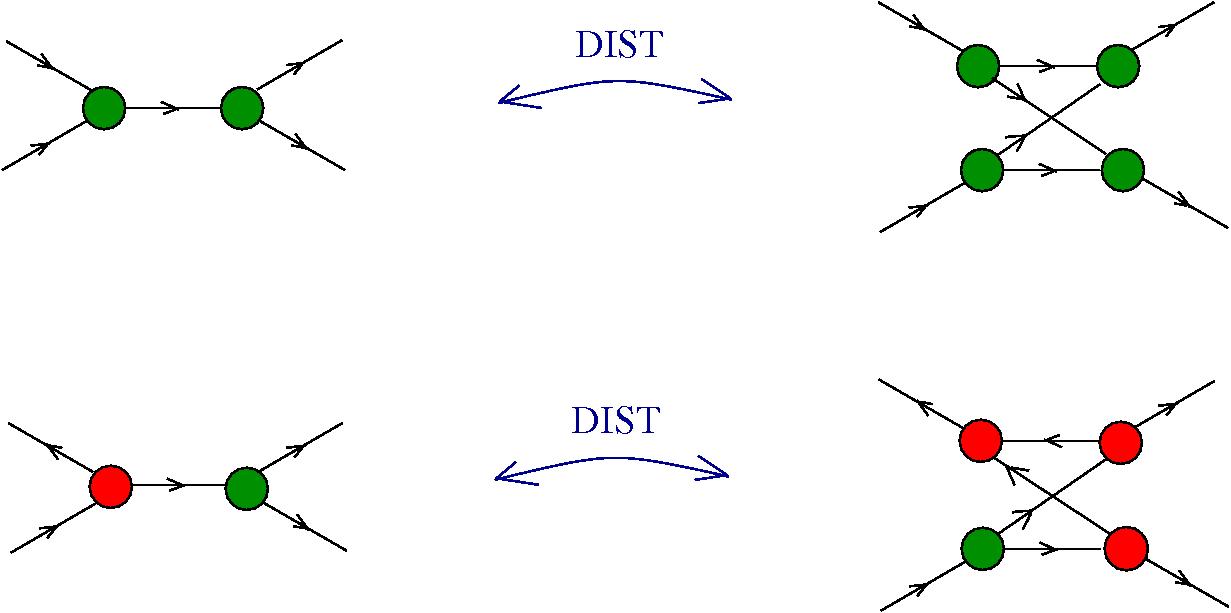
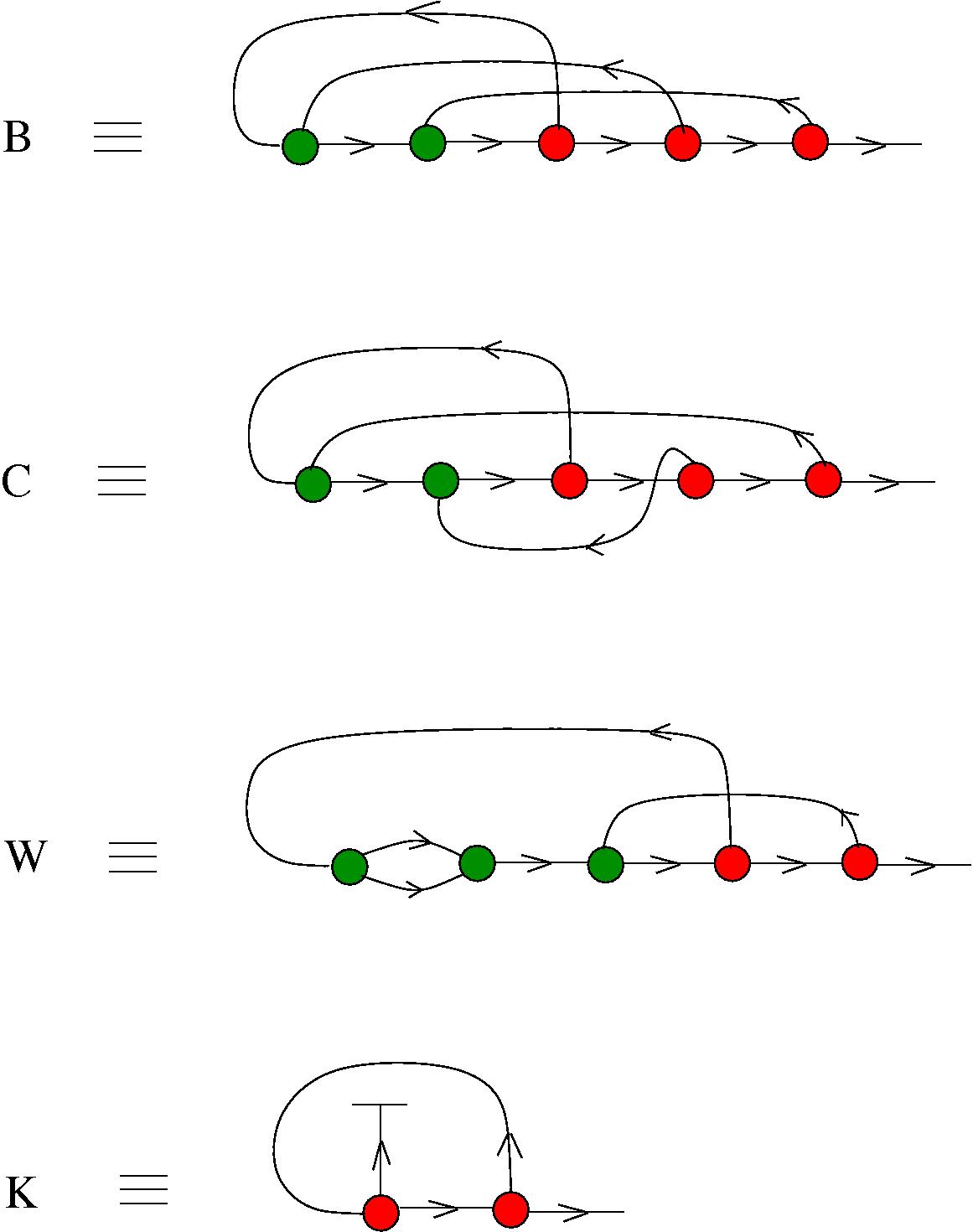
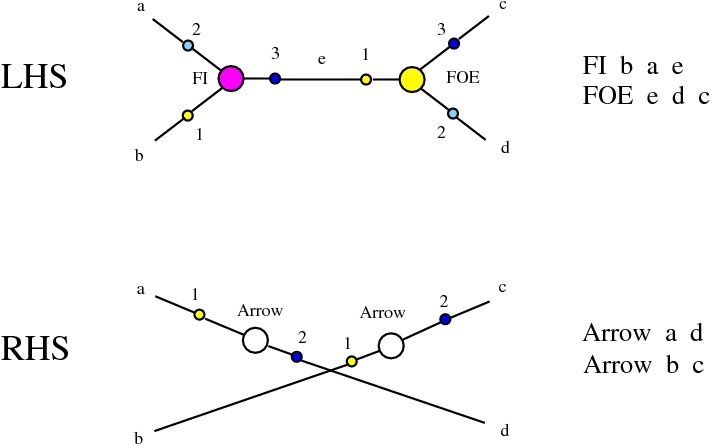
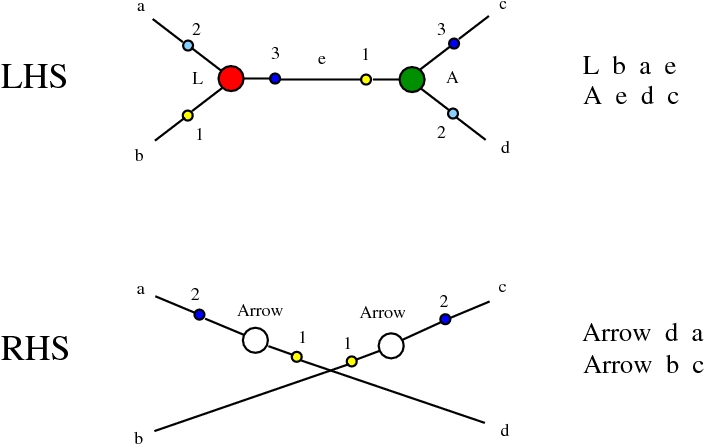
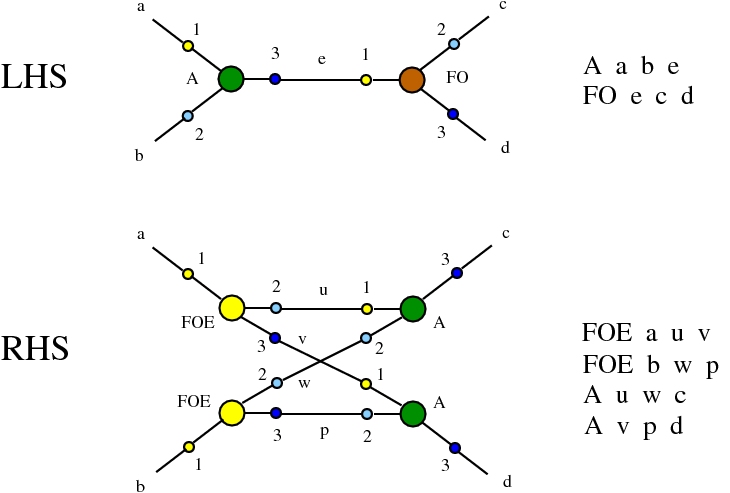
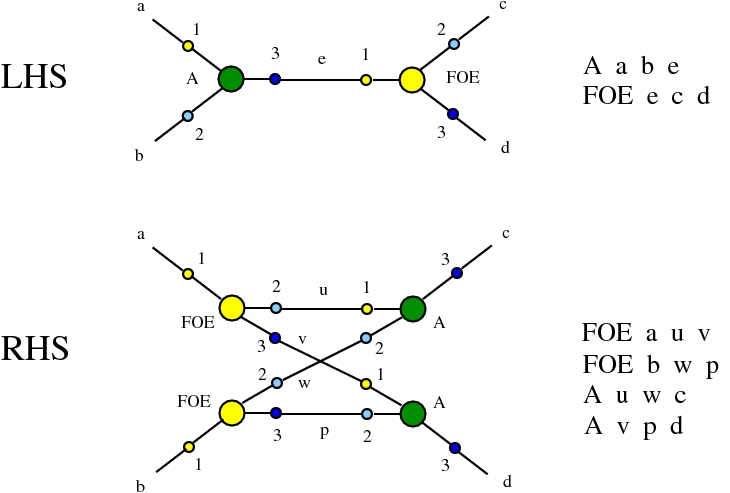
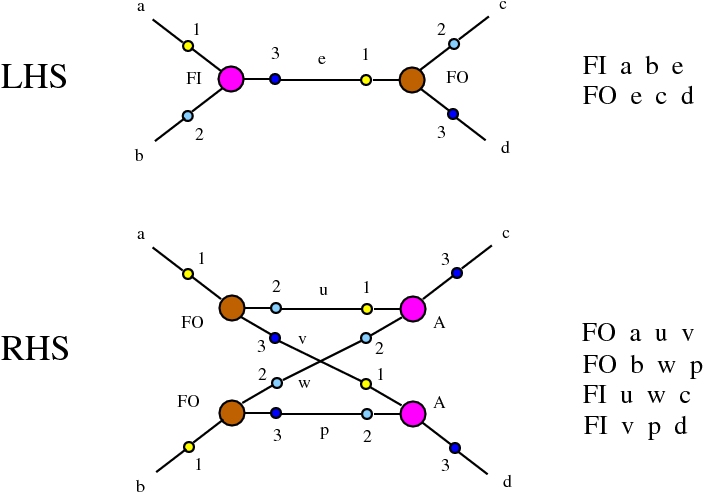
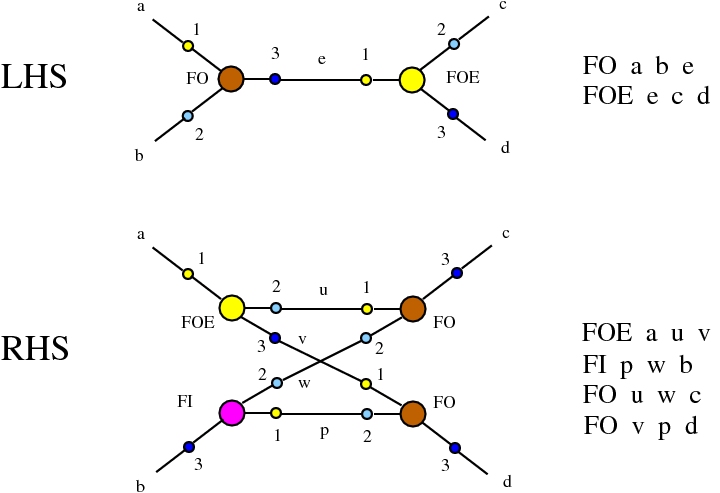
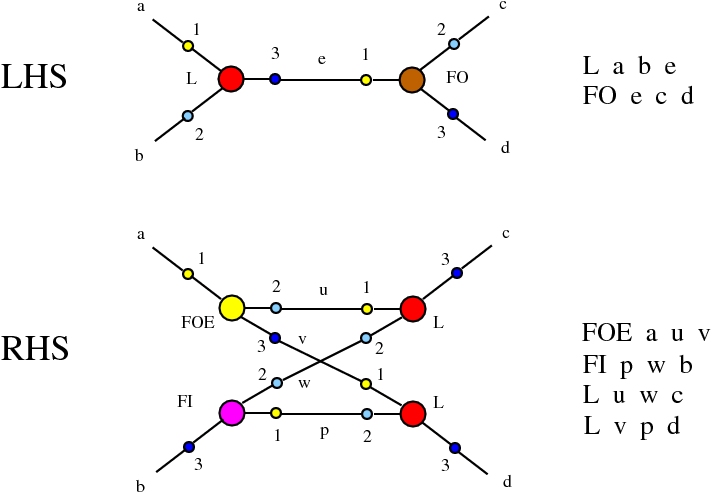
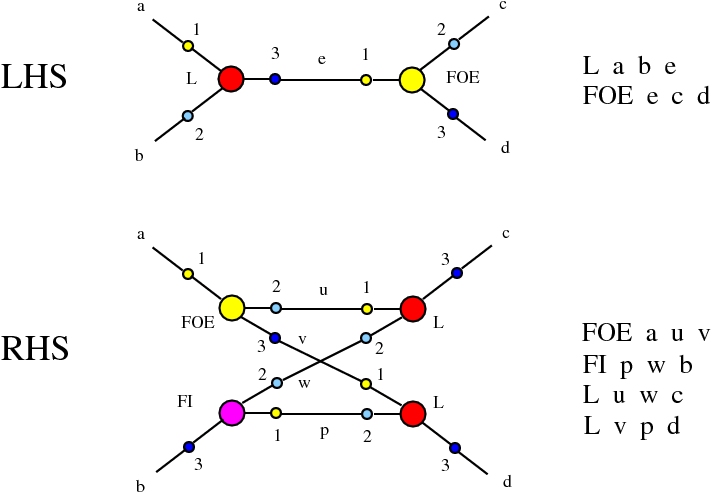
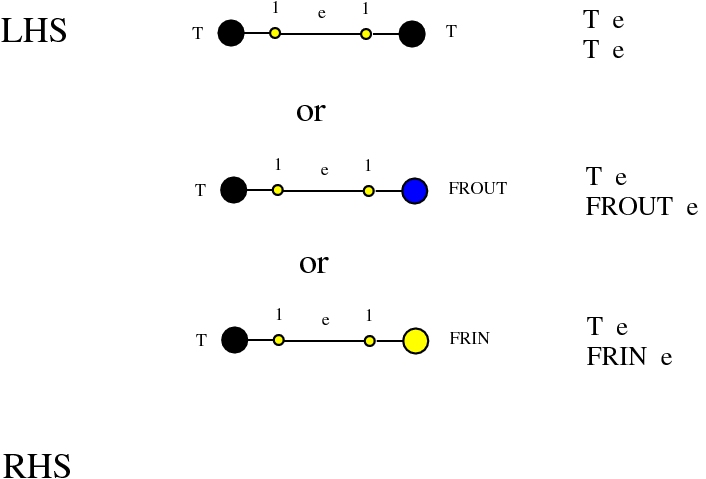
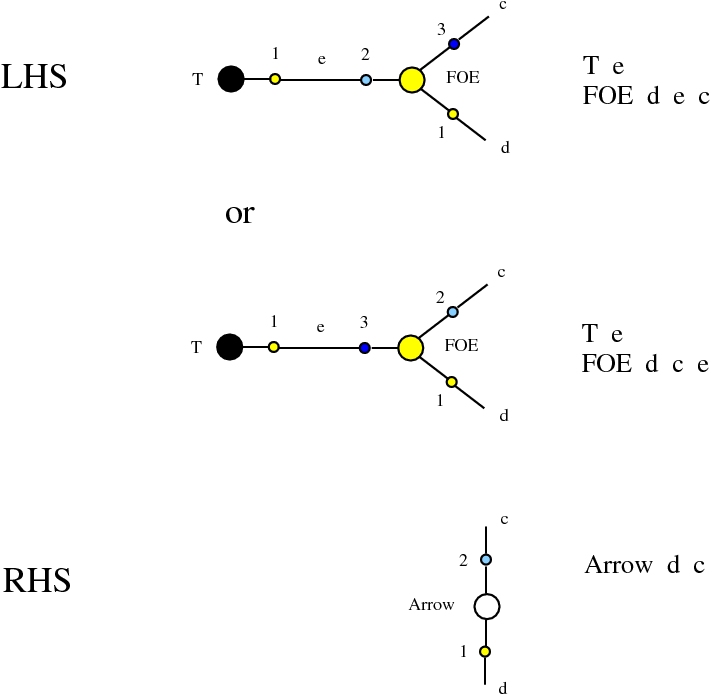
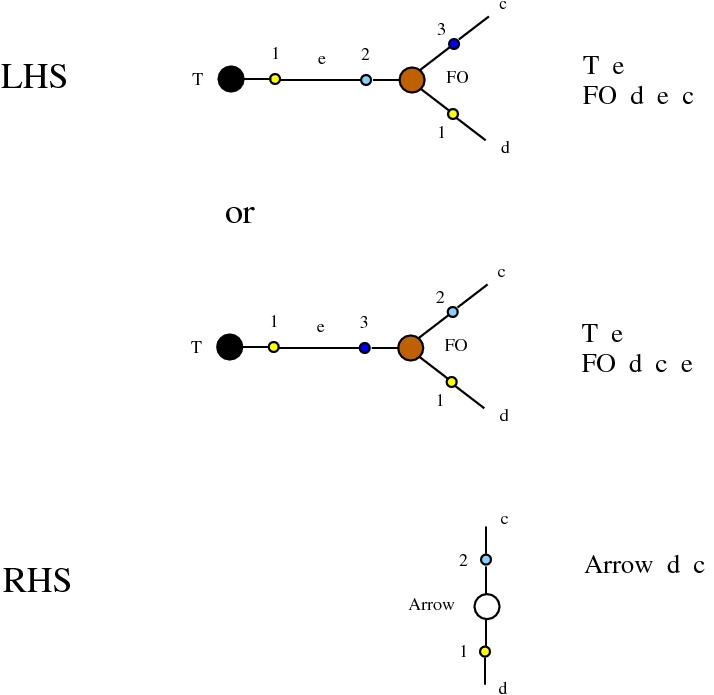
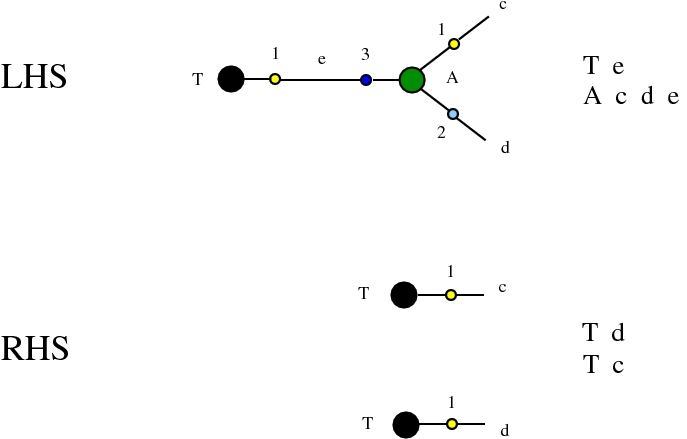
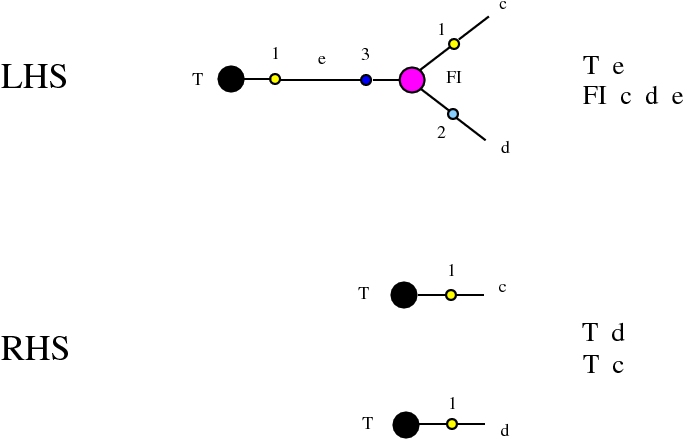
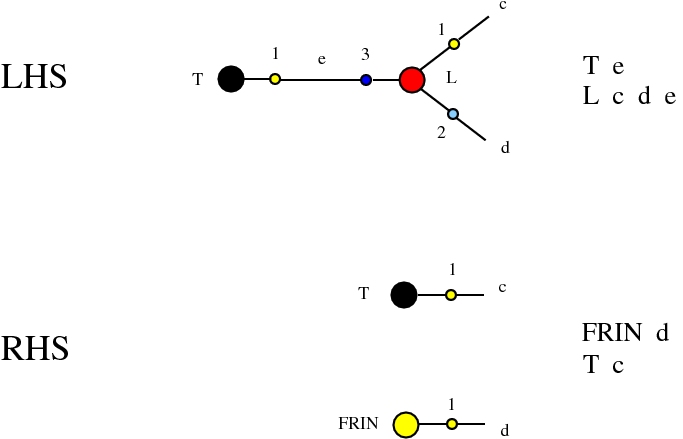
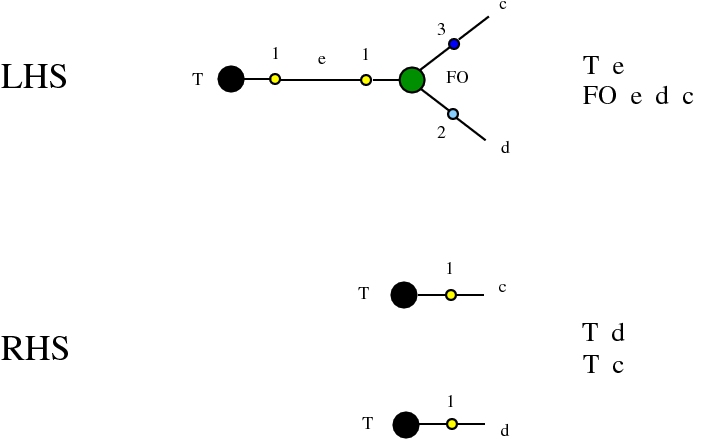
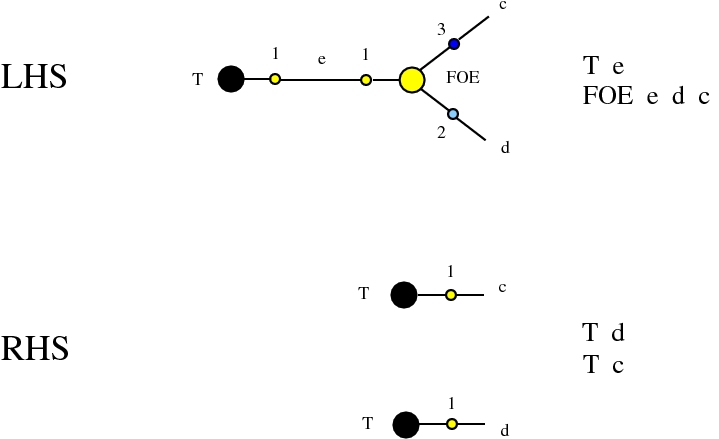
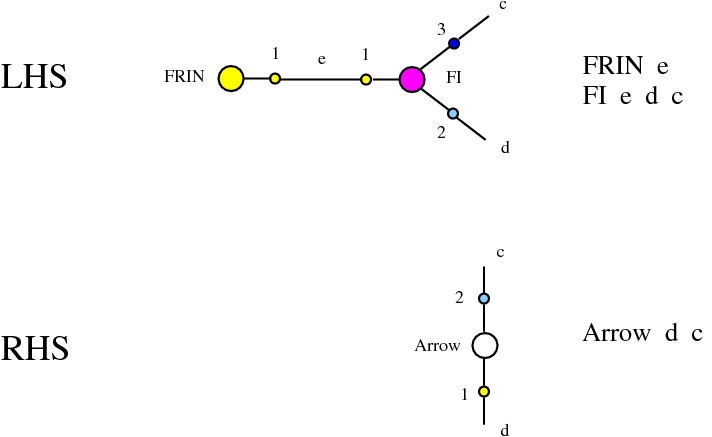
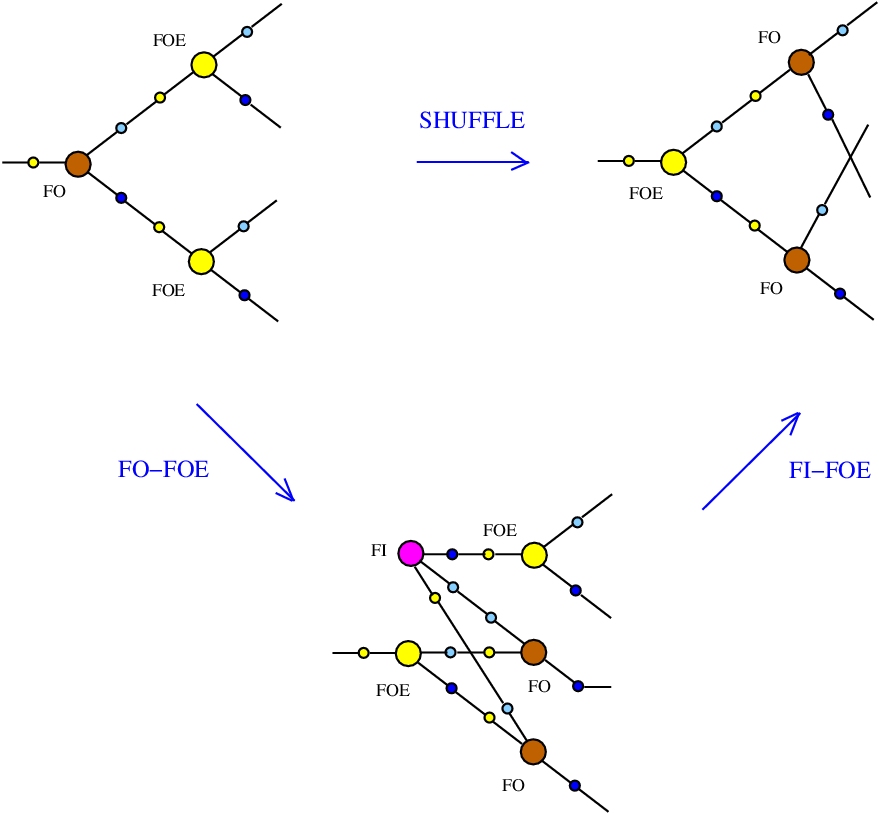
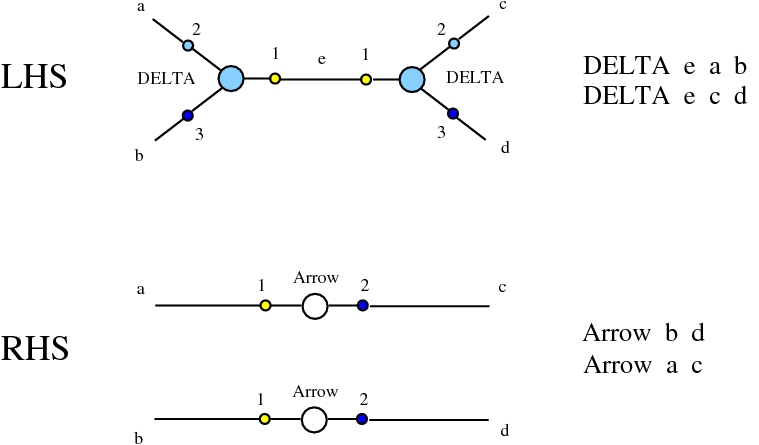
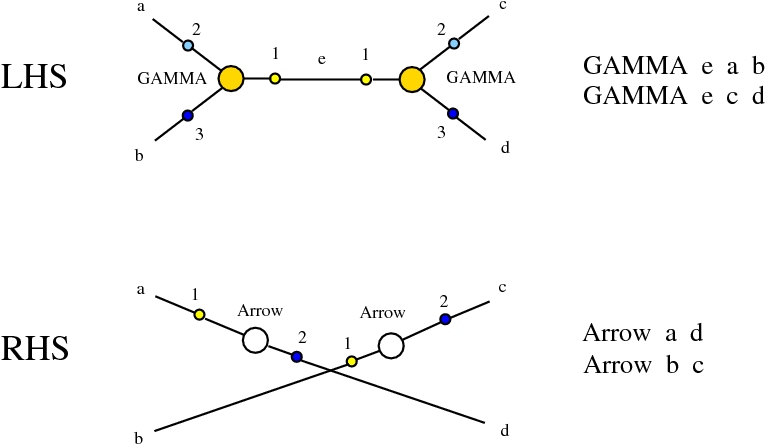
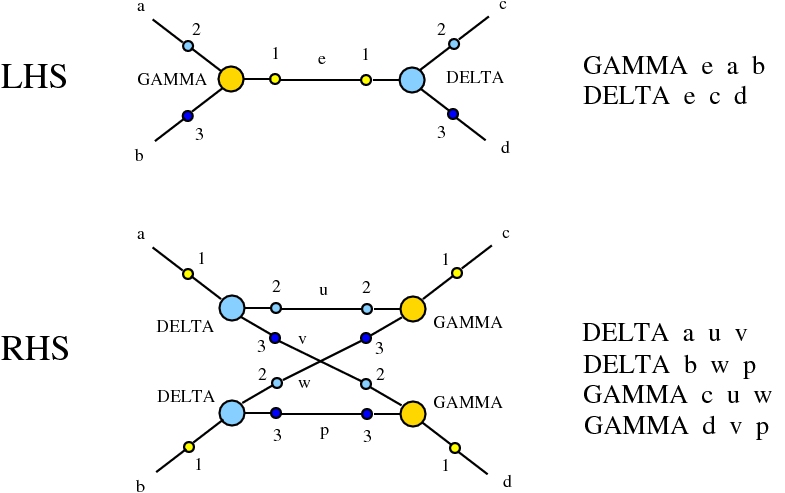
The chemlambda v2 rewrites solve the problem of the curious DISENTANGLE rewrite by introducing two fanout nodes (FO and FOE) instead of one and by a modified set of graph rewrites. These are the following. We use the mol notation for clarity and we describe the rewrites by giving the LHS and RHS patterns:
The DISENTANGLE rewrite is no longer needed, because it's effect can be achieved by the SHUFFLE move, which is a sequence of two chemlambda v2 rewrites: FO-FOE and FI-FOE.
Interaction Combinators, as they appear in chemlambda v2 programs
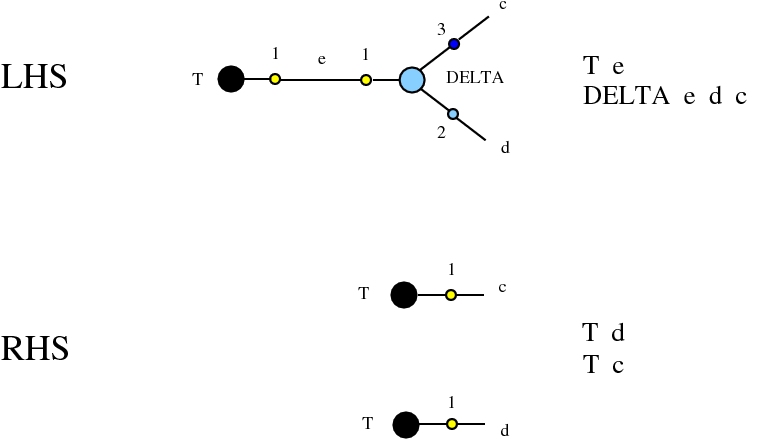
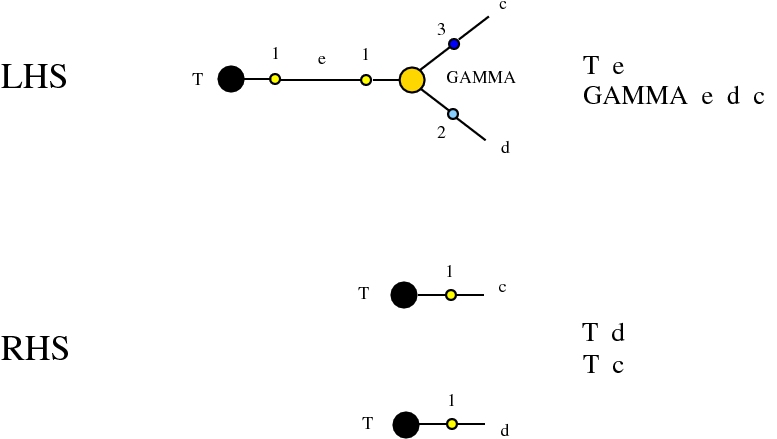
For completeness, here are the graph rewrites of Lafont' Interaction combinators, as they appear in the chemlambda v2 js programs, chemistry IC in chemistry.js:All LHS patterns, of chemlambda and IC, are made of two nodes connected through their active ports. The main difference between chemlambda v2 rewrites and IC rewrites is that several chemlambda nodes have two active ports, while IC nodes have only one active port.
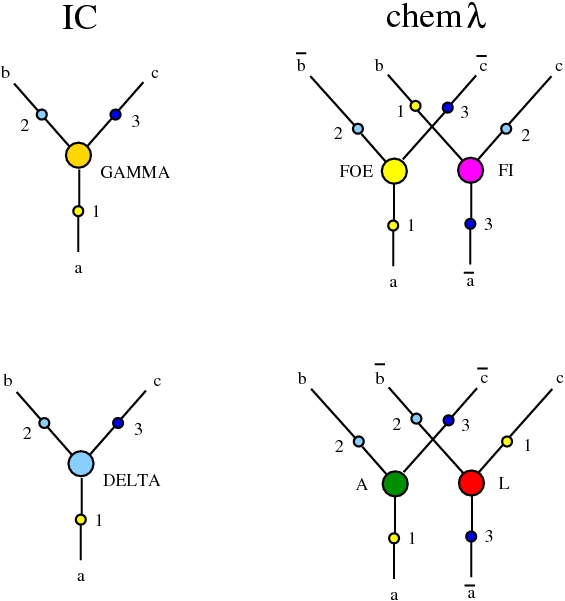
It is possible to modify the chemlambda v2 chemistry such that there are no conflicts. We obtain a chemistry called "dirIC", or directed interaction combinators, explained in
[Alife properties of directed interaction combinators vs. chemlambda. Marius Buliga (2020), https://mbuliga.github.io/quinegraphs/ic-vs-chem.html#icvschem]
over the same set of nodes as chemlambda v2. With the chemistry dirIC, there is a translation between IC nodes of Lafont to chemlambda nodes: